Writing Equations - AP Calculus AB

Card 0 of 3402

Question

$f(x) = \left\{\begin{matrix} cx^2-2x & x<3\ x& x \geq 3 \end{matrix}\right.$

For what values of the constant is the function continuous on $(-\infty, \infty)$ ?

Answer

Both and are continuous in the intervals they are defined. In order for the function to be continuous on the entire real line, we need to have at . Plugging the value in, we get $c \cdot 3^2 - 2 \cdot 3 = 3$ $\Rightarrow 9c-6 =3 \Rightarrow c=1.$

Compare your answer with the correct one above

Question

$f(x) = \left\{\begin{matrix} cx^2-2x & x<3\ x& x \geq 3 \end{matrix}\right.$

For what values of the constant is the function continuous on $(-\infty, \infty)$ ?

Answer

Both and are continuous in the intervals they are defined. In order for the function to be continuous on the entire real line, we need to have at . Plugging the value in, we get $c \cdot 3^2 - 2 \cdot 3 = 3$ $\Rightarrow 9c-6 =3 \Rightarrow c=1.$

Compare your answer with the correct one above

Question

$f(x) = \left\{\begin{matrix} cx^2-2x & x<3\ x& x \geq 3 \end{matrix}\right.$

For what values of the constant is the function continuous on $(-\infty, \infty)$ ?

Answer

Both and are continuous in the intervals they are defined. In order for the function to be continuous on the entire real line, we need to have at . Plugging the value in, we get $c \cdot 3^2 - 2 \cdot 3 = 3$ $\Rightarrow 9c-6 =3 \Rightarrow c=1.$

Compare your answer with the correct one above

Question

$f(x) = \left\{\begin{matrix} cx^2-2x & x<3\ x& x \geq 3 \end{matrix}\right.$

For what values of the constant is the function continuous on $(-\infty, \infty)$ ?

Answer

Both and are continuous in the intervals they are defined. In order for the function to be continuous on the entire real line, we need to have at . Plugging the value in, we get $c \cdot 3^2 - 2 \cdot 3 = 3$ $\Rightarrow 9c-6 =3 \Rightarrow c=1.$

Compare your answer with the correct one above

Question

$f(x) = \left\{\begin{matrix} cx^2-2x & x<3\ x& x \geq 3 \end{matrix}\right.$

For what values of the constant is the function continuous on $(-\infty, \infty)$ ?

Answer

Both and are continuous in the intervals they are defined. In order for the function to be continuous on the entire real line, we need to have at . Plugging the value in, we get $c \cdot 3^2 - 2 \cdot 3 = 3$ $\Rightarrow 9c-6 =3 \Rightarrow c=1.$

Compare your answer with the correct one above

Question

$f(x) = \left\{\begin{matrix} cx^2-2x & x<3\ x& x \geq 3 \end{matrix}\right.$

For what values of the constant is the function continuous on $(-\infty, \infty)$ ?

Answer

Both and are continuous in the intervals they are defined. In order for the function to be continuous on the entire real line, we need to have at . Plugging the value in, we get $c \cdot 3^2 - 2 \cdot 3 = 3$ $\Rightarrow 9c-6 =3 \Rightarrow c=1.$

Compare your answer with the correct one above

Question

$f(x) = \left\{\begin{matrix} cx^2-2x & x<3\ x& x \geq 3 \end{matrix}\right.$

For what values of the constant is the function continuous on $(-\infty, \infty)$ ?

Answer

Both and are continuous in the intervals they are defined. In order for the function to be continuous on the entire real line, we need to have at . Plugging the value in, we get $c \cdot 3^2 - 2 \cdot 3 = 3$ $\Rightarrow 9c-6 =3 \Rightarrow c=1.$

Compare your answer with the correct one above

Question

$f(x) = \left\{\begin{matrix} cx^2-2x & x<3\ x& x \geq 3 \end{matrix}\right.$

For what values of the constant is the function continuous on $(-\infty, \infty)$ ?

Answer

Both and are continuous in the intervals they are defined. In order for the function to be continuous on the entire real line, we need to have at . Plugging the value in, we get $c \cdot 3^2 - 2 \cdot 3 = 3$ $\Rightarrow 9c-6 =3 \Rightarrow c=1.$

Compare your answer with the correct one above

Question

$f(x) = \left\{\begin{matrix} cx^2-2x & x<3\ x& x \geq 3 \end{matrix}\right.$

For what values of the constant is the function continuous on $(-\infty, \infty)$ ?

Answer

Both and are continuous in the intervals they are defined. In order for the function to be continuous on the entire real line, we need to have at . Plugging the value in, we get $c \cdot 3^2 - 2 \cdot 3 = 3$ $\Rightarrow 9c-6 =3 \Rightarrow c=1.$

Compare your answer with the correct one above

Question

$f(x) = \left\{\begin{matrix} cx^2-2x & x<3\ x& x \geq 3 \end{matrix}\right.$

For what values of the constant is the function continuous on $(-\infty, \infty)$ ?

Answer

Both and are continuous in the intervals they are defined. In order for the function to be continuous on the entire real line, we need to have at . Plugging the value in, we get $c \cdot 3^2 - 2 \cdot 3 = 3$ $\Rightarrow 9c-6 =3 \Rightarrow c=1.$

Compare your answer with the correct one above

Question

$f(x) = \left\{\begin{matrix} cx^2-2x & x<3\ x& x \geq 3 \end{matrix}\right.$

For what values of the constant is the function continuous on $(-\infty, \infty)$ ?

Answer

Both and are continuous in the intervals they are defined. In order for the function to be continuous on the entire real line, we need to have at . Plugging the value in, we get $c \cdot 3^2 - 2 \cdot 3 = 3$ $\Rightarrow 9c-6 =3 \Rightarrow c=1.$

Compare your answer with the correct one above

Question

$f(x) = \left\{\begin{matrix} cx^2-2x & x<3\ x& x \geq 3 \end{matrix}\right.$

For what values of the constant is the function continuous on $(-\infty, \infty)$ ?

Answer

Both and are continuous in the intervals they are defined. In order for the function to be continuous on the entire real line, we need to have at . Plugging the value in, we get $c \cdot 3^2 - 2 \cdot 3 = 3$ $\Rightarrow 9c-6 =3 \Rightarrow c=1.$

Compare your answer with the correct one above

Question

$f(x) = \left\{\begin{matrix} cx^2-2x & x<3\ x& x \geq 3 \end{matrix}\right.$

For what values of the constant is the function continuous on $(-\infty, \infty)$ ?

Answer

Both and are continuous in the intervals they are defined. In order for the function to be continuous on the entire real line, we need to have at . Plugging the value in, we get $c \cdot 3^2 - 2 \cdot 3 = 3$ $\Rightarrow 9c-6 =3 \Rightarrow c=1.$

Compare your answer with the correct one above

Question

$f(x) = \left\{\begin{matrix} cx^2-2x & x<3\ x& x \geq 3 \end{matrix}\right.$

For what values of the constant is the function continuous on $(-\infty, \infty)$ ?

Answer

Both and are continuous in the intervals they are defined. In order for the function to be continuous on the entire real line, we need to have at . Plugging the value in, we get $c \cdot 3^2 - 2 \cdot 3 = 3$ $\Rightarrow 9c-6 =3 \Rightarrow c=1.$

Compare your answer with the correct one above

Question

What is the equation of the tangent line at x = 15 for f(x) = x4 + 5x2 + 44x – 3?

Answer

First we must solve for the general derivative of f(x) = f(x) = x4 + 5x2 + 44x – 3.

f'(x) = 4x3 + 10x + 44

Now, the slope of the tangent line for f(15) is equal to f'(15):

f'(15) = 4(15)3 + 10 15 + 44 = 13694.

To find the tangent line, we need at least one point on the line. To find this, we can use f(15) to get the y value of the point of tangency, which will suffice for our use:

f(15) = 154 + 5(15)2 + 44 15 – 3 = 50625 + 1125 + 660 – 3 = 52407

Now, using the point-slope form of the line, we get:

y - 52407 = 13694 * (x – 15)

Simplify:

y – 52407 = 13694x – 205410

y = 13694x – 153003

Compare your answer with the correct one above

Question

Determine given that .

Answer

This problem requires you to evaluate an indefinite integral of the given function f’(x). Integrating each term of the function with respect to x, we simply divide each coefficient by (n+1), where n is the value of the exponent on x for that particular term, and then add 1 to the value of the exponent on each x. This gives us:

$f(x)=\int f'(x)dx=\int (15x^4+14x^3-9x^2+5x-16)dx$

$f(x)=3x^5+\frac{7}{2}x^4-3x^3+\frac{5}{2}x^2-16x+C$

A correct answer must include a constant C, as the original function may have had a constant that is not reflected in the equation for its derivative.

Compare your answer with the correct one above

Question

What is the area under the curve for ?

Answer

By normal exponent rules $2^x = e^{x \ln 2}$ , and so we set up the definite integral

$\int_{-\infty}^{0} e^{x \ln 2} ~dx$ ,

which integrates to:

$\left[ \frac{e^{x \ln 2}}{\ln 2}\right]_{-\infty}^0 = \frac{2^0 - 2^{-\infty}}{\ln 2} = \frac{1 - 0}{\ln 2}$

Compare your answer with the correct one above

Question

The Gaussian integral formula states that

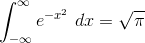$\int_{-\infty}^{\infty} e^{-x^2} ~ dx = \sqrt{\pi}$ .

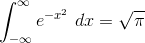
What is the integral of

$\int_{-\infty}^{\infty} x^2 ~ e^{-x^2} ~ dx$ ?

Answer

Integrating by parts with

,

$v = - \frac{1}{2} e^{-x^2}$ , $dv = x ~e^{-x^2}~dx$ ,

we get:

$\int_{-\infty}^{\infty} x^2 e^{-x^2} dx = \int_A^B u ~ dv = \left[ u v\right ]_A^B - \int_A^B v ~ du$

$= \left[ \frac{-x}{2} e^{-x^2} \right ]_{-\infty}^{\infty} - \int_{-\infty}^{\infty} \frac{-1}{2} e^{-x^2}~ dx = [0 - 0] - \frac{-1}{2} \sqrt{\pi} = \frac{\sqrt{\pi}}{2}$

Compare your answer with the correct one above

Question

What is the value of the following definite integral?

$\int_{0}^{\pi /2}\bigg(-5sin(x)-3cos(x)+\frac{4}{\pi }\bigg)dx$

Answer

We start by integrating the function in parentheses with respect to x, and we then subtract the evaluation of the lower limit from the evaluation of the upper limit:

$\int_{0}^{\pi /2}\bigg(-5sin(x)-3cos(x)+\frac{4}{\pi })dx=(5cos(x)-3sin(x)+\frac{4}{\pi }x\bigg)_{0}^{\pi /2}$

$=(5cos(\frac{\pi }{2})-3sin(\frac{\pi }{2})+\frac{4}{\pi }(\frac{\pi }{2}))-(5cos(0)-3sin(0)+\frac{4}{\pi}(0))$

Compare your answer with the correct one above

Question

Determine the amount of work required to push a box from meters to meters, given the function for force below:

$F(x)=x^2-sin(2x)+\frac{1}{x}$

Answer

This problem intends to demonstrate one possible application of calculus to the field of physics. An equation for work as given in physics is as follows:

$W=\int F(x)dx$

Using this equation, we simply set up a definite integral with our bounds given by the interval of interest in the problem:

$W=\int_{2}^{5}\bigg(x^2-sin(2x)+\frac{1}{x}\bigg)dx$

$W=\bigg(\frac{1}{3}x^3+\frac{1}{2}cos(2x)+ln(x)\bigg)_{2}^{5}$

$W=\bigg(\frac{1}{3}(5)^3+\frac{1}{2}cos(10)+ln(5)\bigg)-\bigg(\frac{1}{3}(2)^3+\frac{1}{2}cos(4)+ln(2)\bigg)$

Joules

After evaluating our integral, we can see that the work required to push the box from x=2 meters to x=5 meters is 39.8 Joules.

Compare your answer with the correct one above

Tap the card to reveal the answer