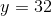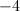How to find out when an equation has no solution

Expand out into .

Since , it can be seen that

so Quantity B is greater.

First, distribute the to the terms inside the parentheses.

Add 6x to both sides.

This is false for any value of . Thus, there is no solution.

Let us write down what we are told in mathematical terms, designating the smaller integer as and the larger integer as .

The sum of the two integers is :

And the larger integer is % greater than the smaller integer:

Writing the first equation in terms of gives:

Which allows us to find :

Thus, the positive difference between the two is found as

By definition, the absolute value of an expression can never be less than 0. Therefore, there are no solutions to the above expression.

We are given that y = 32. Plug this value of y into the second equation.

32 = x2 – 4

36 = x2

x = +/– 6.

Next find a value for Quantity A:

y/7 = 32/7

This number is less than +6, but more than –6. Thus, the relationship cannot be determined from the information given.

To solve this problem, expand each function described by Quantities A and B:

Quantity A:

Quantity B:

Now note that Quantities A and B only differ in that Quantity A is greater by .

Since we are told that is greater than and thus always positive, Quantity A must be greater than Quantity B for all possible values of .

Substituting 3 in for x, you will get 0 in the denominator of the fraction. It is not possible to have 0 be the denominator for a fraction so there is no possible solution to this equation.

A fraction is considered undefined when the denominator equals 0. Set the denominator equal to zero and solve for the variable.