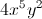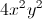How to simplify square roots
PSAT Math · Learn by Concept
Help Questions
PSAT Math › How to simplify square roots
Simplify. Assume all integers are positive real numbers.
Explanation
Index of 
Find a perfect cube in 

Simplify the perfect cube, giving you ![2\sqrt[3]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/25876/gif.latex)
Take your exponents on both variables and determine the number of times our index will evenly go into both.
The final answer would be
Simplify:
Explanation
4√27 + 16√75 +3√12 =
4*(√3)*(√9) + 16*(√3)*(√25) +3*(√3)*(√4) =
4*(√3)*(3) + 16*(√3)*(5) + 3*(√3)*(2) =
12√3 + 80√3 +6√3= 98√3
Simplify
9 ÷ √3
3√3
3
2
not possible
none of these
Explanation
in order to simplify a square root on the bottom, multiply top and bottom by the root

Simplify:
√192
8√2
8√3
4√3
4√2
None of these
Explanation
√192 = √2 X √96
√96 = √2 X √48
√48 = √4 X√12
√12 = √4 X √3
√192 = √(2X2X4X4) X √3
= √4X√4X√4 X √3
= 8√3
What is the simplest way to express 
Explanation
First we will list the factors of 3888:
Simplify:
Explanation
To simplify a square root, you can break the number down into its prime factors using a factor tree. The prime factors of 72 are 
The square root of 


The square root of 

When you multiply together your answers,
Simplify square roots. Assume all integers are positive real numbers.
Simplify as much as possible. List all possible answers.
1a.
1b.
1c.
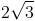
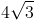





Explanation
When simplifying radicans (integers under the radical symbol), we first want to look for a perfect square. For example, 


1a.
Do the same thing for 
1b.
1c.Follow the same procedure except now you are looking for perfect cubes.
Simplify. Assume all variables are positive real numbers.
Explanation
The index coefficent in ![\sqrt[n]{b}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/25860/gif.latex)


First look for a perfect square,
Then to your Variables
Take your exponents on both variables and determine the number of times our index will evenly go into both.
So you would take out a 
*Dividing the radican exponent by the index - gives you the number of variables that should be pulled out.
The final answer would be 
Simplify:
√112
12
20
4√10
10√12
4√7
Explanation
√112 = {√2 * √56} = {√2 * √2 * √28} = {2√28} = {2√4 * √7} = 4√7
![\sqrt[3]{24x^{16}y^{12}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/25869/gif.latex)
![2x^{5}y^{4}\sqrt[3]{3x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/32040/gif.latex)

![2x^{8}y^{4}\sqrt[3]{3x^{2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/32044/gif.latex)
![2x^{2}y^{3}\sqrt[3]{3xy}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/32046/gif.latex)

![\sqrt[3]{24x^{16}y^{12}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/25870/gif.latex)

![\sqrt[3]{8\cdot 3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/25875/gif.latex)
![x\rightarrow \frac{16}{3}= 5^{\frac{1}{3}} \rightarrow x^{5}\sqrt[3]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/25877/gif.latex)

![2x^{5}y^{4}\sqrt[3]{3x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/25879/gif.latex)





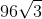
















![\sqrt[3]{24}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/25945/gif.latex)
![2\sqrt[3]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/32078/gif.latex)
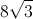
![2\sqrt[3]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/32084/gif.latex)
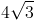


![\sqrt[3]{24}=\sqrt[3]{8\cdot 3}=\sqrt[3]{8}\cdot\sqrt[3]{3}=2\sqrt[3]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/25952/gif.latex)