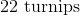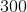How to find a ratio
SSAT Middle Level: Quantitative · Learn by Concept
Help Questions
SSAT Middle Level: Quantitative › How to find a ratio
A soccer team played 20 games, winning 5 of them. The ratio of wins to losses is
Explanation
The ratio of wins to losses requires knowing the number of wins and losses. The question says that there are 5 wins. That means there must have been

The ratio of wins to losses is thus 5 to 15 or 1 to 3.
At a local microchip factory, there are 


Explanation
In order to solve this problem, we will create a table of proportions using the following ratio.
If we solve for the table, then we can find the number of managers needed for 

The factory will need 
A motorcycle travels 

Explanation
In order to find the motorcyclist’s speed, we need to create a ratio of the miles travelled in a single hour.
Reduce and solve.
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Explanation
Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Explanation
Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Explanation
Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Explanation
Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Write as a unit rate: 






Explanation
Divide the number of revolutions by the number of minutes to get revolutions per minute:

making 
Candidate A receives 


Explanation
In order to solve this problem we need to create a ratio with the given information. It says that for every 

Now substitute in the given numbers.
We know that candidate B received 
Now, use the original relationship to create a proportion and solve for the number of votes that candidate A received.
Cross multiply and solve for 
Simplify and solve.
Candidate A receives 


Explanation
In order to solve this problem we need to create a ratio with the given information. It says that for every 

Now substitute in the given numbers.
We know that candidate B received 
Now, use the original relationship to create a proportion and solve for the number of votes that candidate A received.
Cross multiply and solve for 
Simplify and solve.